ชุดข้อมูลตารางแปลงลาปลาซที่ครอบคลุม
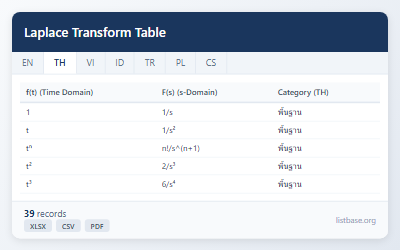
ชุดข้อมูลนี้มีตารางคู่การแปลงลาปลาซที่ครอบคลุม 39 รายการ โดยแมปฟังก์ชันจากโดเมนเวลา (f(t)) ไปยังโดเมน s (F(s)) รวมถึงหมวดหมู่ เงื่อนไข และคำอธิบาย.
ดาวน์โหลดฟรี
ประเด็นสำคัญ
- เข้าถึงคู่การแปลงลาปลาซที่จำเป็น 39 รายการเพื่อการอ้างอิงอย่างรวดเร็ว
- สำรวจฟังก์ชันทั่วไปและสิ่งที่เทียบเท่าในโดเมน s
- ดาวน์โหลดตารางที่สมบูรณ์ในหลายรูปแบบที่สะดวก
- ใช้ประโยชน์จากข้อมูลนี้สำหรับการศึกษาด้านวิศวกรรม ฟิสิกส์ และคณิตศาสตร์
แสดง 39 จาก 39
| Category | f(t) (Time Domain) | F(s) (s-Domain) | Condition | Description |
|---|---|---|---|---|
| พื้นฐาน | 1 | 1/s | s > 0 | ขั้นหน่วย (ค่าคงที่) |
| พื้นฐาน | t | 1/s² | s > 0 | ฟังก์ชันทางลาด |
| พื้นฐาน | tⁿ | n!/s^(n+1) | s > 0, n ≥ 0 | ฟังก์ชันกำลัง |
| พื้นฐาน | t² | 2/s³ | s > 0 | กำลังสอง |
| พื้นฐาน | t³ | 6/s⁴ | s > 0 | กำลังสาม |
| พื้นฐาน | √t | √π/(2s^(3/2)) | s > 0 | รากที่สอง |
| ฟังก์ชันชี้กำลัง | e^(at) | 1/(s-a) | s > a | ฟังก์ชันชี้กำลัง |
| ฟังก์ชันชี้กำลัง | t·e^(at) | 1/(s-a)² | s > a | ฟังก์ชันทางลาดชี้กำลัง |
| ฟังก์ชันชี้กำลัง | tⁿ·e^(at) | n!/(s-a)^(n+1) | s > a | กำลังชี้กำลัง |
| ฟังก์ชันชี้กำลัง | 1 - e^(-at) | a/(s(s+a)) | s > 0 | การลดลงแบบชี้กำลังจาก 1 |
| ตรีโกณมิติ | sin(ωt) | ω/(s²+ω²) | s > 0 | ฟังก์ชันไซน์ |
| ตรีโกณมิติ | cos(ωt) | s/(s²+ω²) | s > 0 | ฟังก์ชันโคไซน์ |
| ตรีโกณมิติ | tan(ωt) | Complex | - | แทนเจนต์ (ไม่มีรูปแบบง่าย) |
| ตรีโกณมิติ | t·sin(ωt) | 2ωs/(s²+ω²)² | s > 0 | ไซน์ทางลาด |
| ตรีโกณมิติ | t·cos(ωt) | (s²-ω²)/(s²+ω²)² | s > 0 | โคไซน์ทางลาด |
| ตรีโกณมิติ | sin²(ωt) | 2ω²/(s(s²+4ω²)) | s > 0 | ไซน์กำลังสอง |
| ตรีโกณมิติ | cos²(ωt) | (s²+2ω²)/(s(s²+4ω²)) | s > 0 | โคไซน์กำลังสอง |
| หน่วง | e^(-at)·sin(ωt) | ω/((s+a)²+ω²) | s > -a | ไซน์หน่วง |
| หน่วง | e^(-at)·cos(ωt) | (s+a)/((s+a)²+ω²) | s > -a | โคไซน์หน่วง |
| ไฮเพอร์โบลิก | sinh(at) | a/(s²-a²) | s > |a| | ไฮเพอร์โบลิกไซน์ |
| ไฮเพอร์โบลิก | cosh(at) | s/(s²-a²) | s > |a| | โคไซน์ไฮเพอร์โบลิก |
| พิเศษ | δ(t) | 1 | all s | ฟังก์ชันดิแรกเดลตา (อิมพัลส์) |
| พิเศษ | δ(t-a) | e^(-as) | all s | อิมพัลส์หน่วงเวลา |
| พิเศษ | u(t) | 1/s | s > 0 | ฟังก์ชันขั้นบันไดหนึ่งหน่วย |
| พิเศษ | u(t-a) | e^(-as)/s | s > 0 | ขั้นบันไดหน่วงเวลา |
| เบสเซล | J₀(at) | 1/√(s²+a²) | s > 0 | ฟังก์ชันเบสเซล J₀ |
| เบสเซล | J₁(at) | (√(s²+a²)-s)/(a√(s²+a²)) | s > 0 | ฟังก์ชันเบสเซล J₁ |
| ลอการิทึม | ln(t) | -(ln(s)+γ)/s | s > 0 | ลอการิทึมธรรมชาติ (γ = ออยเลอร์) |
| ลอการิทึม | (1-e^(-t))/t | ln((s+1)/s) | s > 0 | รูปแบบลอการิทึม |
| ฟังก์ชันความคลาดเคลื่อน | erf(√t) | 1/(s√(s+1)) | s > 0 | ฟังก์ชันความคลาดเคลื่อน |
| ฟังก์ชันความคลาดเคลื่อน | erfc(√t) | 1/s - 1/(s√(s+1)) | s > 0 | ความคลาดเคลื่อนส่วนเติมเต็ม |
| คุณสมบัติ | f'(t) | s·F(s) - f(0) | - | อนุพันธ์อันดับหนึ่ง |
| คุณสมบัติ | f''(t) | s²·F(s) - s·f(0) - f'(0) | - | อนุพันธ์อันดับสอง |
| คุณสมบัติ | ∫f(τ)dτ | F(s)/s | - | การอินทิเกรต |
| คุณสมบัติ | f(t-a)·u(t-a) | e^(-as)·F(s) | a > 0 | การเลื่อนเวลา |
| คุณสมบัติ | e^(at)·f(t) | F(s-a) | - | การเลื่อนความถี่ |
| คุณสมบัติ | t·f(t) | -dF(s)/ds | - | การคูณด้วย t |
| คุณสมบัติ | f(at) | (1/a)·F(s/a) | a > 0 | การปรับขนาดเวลา |
| คุณสมบัติ | f(t)*g(t) | F(s)·G(s) | - | คอนโวลูชัน |
กรณีการใช้งาน
- นำเข้าไฟล์ CSV เข้าสู่สคริปต์ Python หรือซอฟต์แวร์จำลองเพื่อทำให้การคำนวณที่เกี่ยวข้องกับการแปลงลาปลาซเป็นไปโดยอัตโนมัติ.
- ใช้ไฟล์ Excel เพื่อกรองและจัดเรียงคู่การแปลงเฉพาะ สร้างแผ่นอ้างอิงที่กำหนดเอง หรือรวมเข้ากับรายงานทางวิศวกรรม.
- พิมพ์เวอร์ชัน PDF สำหรับการอ้างอิงแบบออฟไลน์อย่างรวดเร็วในระหว่างการสอบ การบรรยาย หรือการแก้ปัญหาเชิงปฏิบัติ.
- รวมชุดข้อมูลนี้เข้ากับแพลตฟอร์มการศึกษาหรือเครื่องมือ e-learning เพื่อให้นักเรียนมีแหล่งข้อมูลการเรียนรู้ที่มีโครงสร้าง.